Un schéma consistant est un schéma tel que l'erreur de troncature tende vers zèro quand h et
tendent vers zéro.
L'ordre du schéma mesure la précision ou l'erreur de troncature mathèmatique commise en remplacant les dérivées partielles exactes par leurs approximations.
On remplacepar la formule aux diffèrence finies :
Pour montrer que ce schèma est consistant, on fait les developpements de Taylor de u en temps et en espace :
On injecte dans l'equation aux dérivées partielles discrétisé :
=
=
+ 
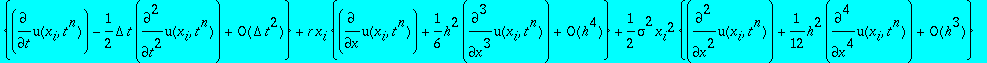
= r u(xi,tn) + E.T. où E.T. est l'erreur de troncature
On à donc que l'erreur de troncature tend vers zèro quand h et
De plus E.T. =, donc le schéma est d'ordre 1 en temps et d'ordre 2 en espace.
Retour sommaire