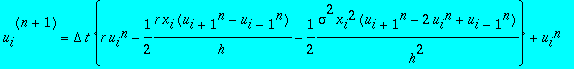Une méthode pour résoudre numériquement le modèle de Black et Scholes consiste à discrétiser le problème continu par différences finies.
                    Rappelons que nous nous sommes placés dans le cas monodimentionnel d'une barre de longueur L pour simplifier. On choisit une discrétisation régulière de [0,L] en intervalle de longueur h tels que L=N.h et une discrétisation de l'intervalle de temps [0,T] en pas de temps de longueur (attention, est négatif)  tels que T=N. . Notons x_i le point i.h et tⁿ le temps n. . Notons  la valeur de la solution approchée au point x _i et au temps t^M-n .

        On construit un maillage uniforme:

                                                                                              h=L/N

^---I^----------I^---------- I^{---------------------------------} I ^---------- I^{-----------------------------------} I ^{------------> x}

  x₀=0         x₁ =h          x ₂ =2h                                           x _i               x _i+1                                             x _N =L

       

        Discrétisation en temps:

      u^M                      u ^M-1                    u ^M-2                                              u ^M-n  =T/N   u ^M-n-1                                      u ⁰          
---I-----------I-----------I-----------------------I ------------I--------------------I---- > t

    t⁰=0                    t¹=            t ² =2                                        t ⁿ                            t ⁿ⁺¹                                     t ^M =T

        Rappelons que le modèle de Black et Scholes est une équation aux dérivées partielles parabolique de la forme :

pour  tout (x,t) appartenant à ]0,L[x]0,T[ condition finale :  pour x appartenant à ]0,L[ conditions limites :  pour t appartenant à ]0,T[                                 pour appartenant à ]0,T[

On cherche à approcher  en utilisant les valeurs de u. Or le développement de Taylor de u en (x _i , t ⁿ⁺¹ ) est :

donc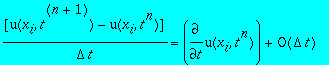  
donc on remplace  par la formule aux différences finies décentrée aval .

On cherche à approcher  en utilisant les valeurs de u. Or le développement de Taylor de u en (x _i+1 , tⁿ ) et  (x , tⁿ ) sont :


donc
donc on remplace  par la formule aux différences finies centrée .

On cherche à approcher  en utilisant les valeurs de u. Or, d'après le développement de Taylor ci-dessus de u en   (x _i+1 ,tⁿ) et  (x _i-1, t ⁿ) on a :

donc on remplace  par la formule aux différences finies centrée .
     

  Donc on remplace  par la formule aux différences finies  consistante .

On cherche à approcher  en utilisant les valeurs de u. Or le développement de Taylor de u en (x _N-1 , t ⁿ ) est :

donc
donc on remplace   par la formule aux différences finies décentrée amont  .

  On obtient alors l'équation aux dérivées partielles discrétisée suivante :

appartenant à {1,2,...,N-1} x {0,1,2,....,M-1} pour i appartenant à {1,2,...,N-1} pour n appartenant à {0,1,2,....,M-1} pour n appartenant à {0,1,2,....,M-1}

        Ce schéma est un schéma à un pas, car les solutions approchées au temps tⁿ⁺¹ ne dépend que des solutions approchées au temps t ⁿ . C'est un schéma explicite car il donne une formule explicite de calcul de la solution au temps tⁿ⁺¹ en fonction des valeurs de la solution au temps précèdent.

Connaissant la solution discrète u(x_i, tⁿ⁺¹) au temps t ⁿ⁺¹, on veut connaître la solution discrète u(x _i , t ⁿ) au temps t ⁿ . On a :

donc
 d'où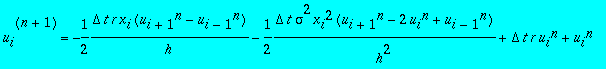
Donc la solution discrète u(x _i , tⁿ) au temps t ⁿ   est obtenu par la relation :
 

Retour sommaire