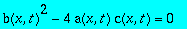L'équation de Black et Scholes qui est :est une équation aux dérivées partielles du second ordre du type : a Uxx+bUxt +cUtt+dUx +eU t +fU=g
avec Uxx qui est la dérivée seconde de U par rapport à x,
U xt qui est la dérivée seconde de U par rapport à x et t,
Utt qui est la dérivée seconde de U par rapport à x et t,
Ux qui est la dérivée première de U par rapport à x,
Ut qui est la dérivée première de U par rapport à t,
où,
,
,
,
et
.
D'où l'équation aux dérivées partielles est linéaire, puisque ces coefficients ne dépendent pas de u(x,t), mais elle n'est pas à coefficients constants car a et d dépendent de x.
De plus, pour tout x et pour tout t appartenant au réel positif on a :donc l'équation aux dérivées partielles est dite parabolique .
Retour sommaire